Lab 13 - Bandwidth and Signal Analysis

Objective
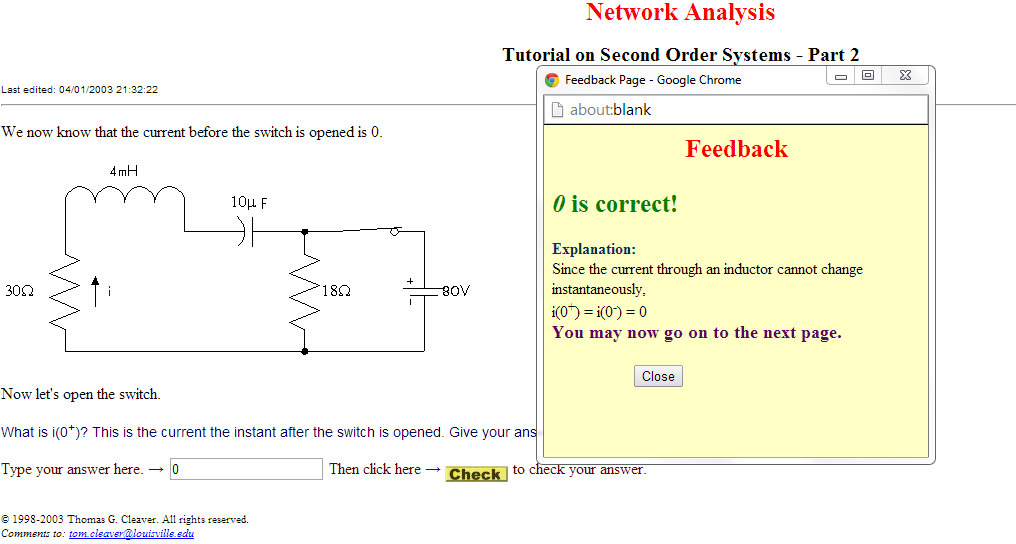
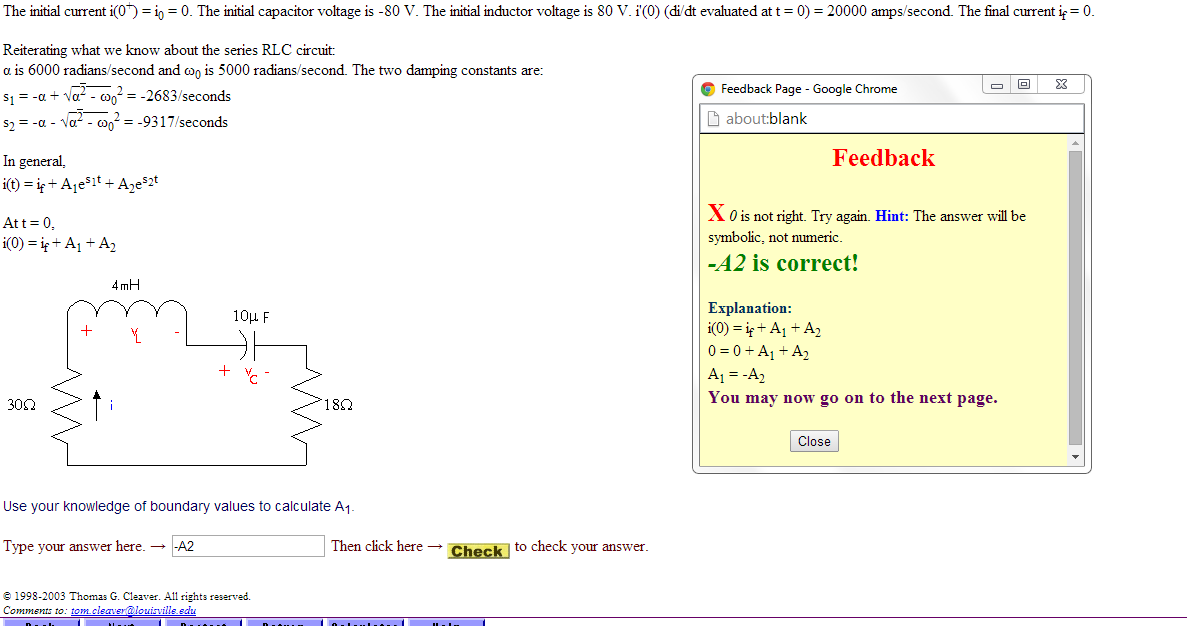
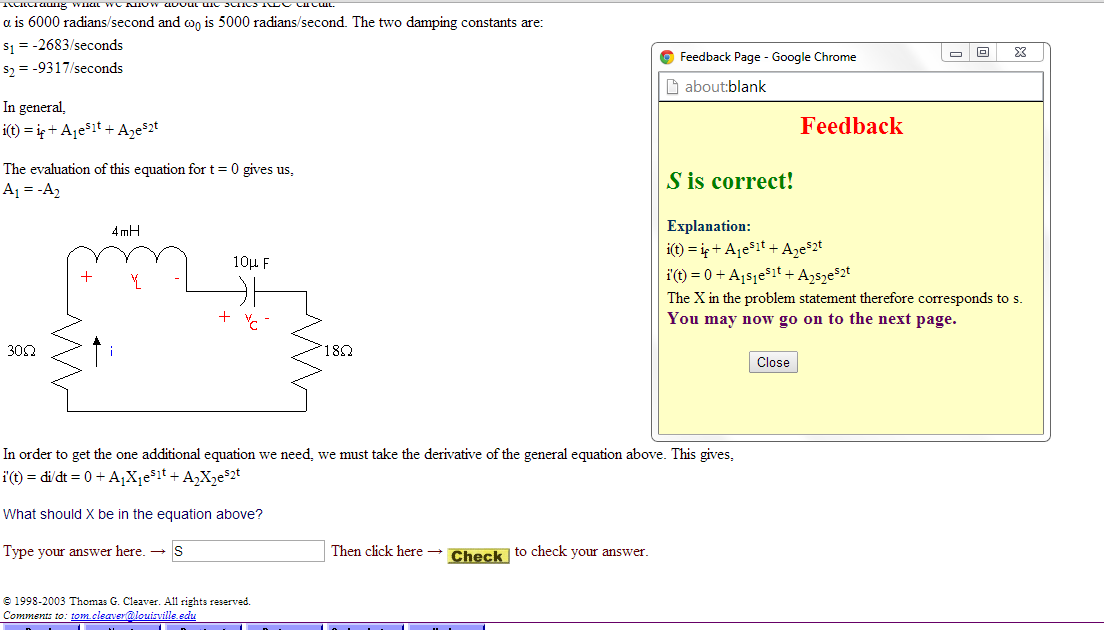
- To understand how bandwidth is determined

Lab
For this lab, a RLC circuit is hooked up with a function generator to determine the bandwidth of the circuit.  Before measuring the actual bandwidth of the circuit, the theoretical values were calculated for two different circuits.  The two circuits use the same inductor value but have different resistors and capacitor values.
Components:
L = 1 mH
R = 100 Ω and  10Ω
C = 100 µF and 1µF

First Circuit

Resonance Frequency = 3162 rad/s

Quality = 0.032

Bandwidth = 98821

ITheoretical = Vm/sqrt(R^2 +(ωL - 1/ωC)^2) 

              = 3.47/sqrt(100^2+(3162*.001-1/(3162*100*10^-6))^2 

              = 34.7mA

IActual  =  34.1mA

Second Circuit

Resonance Frequency = 31622.78 rad/s

Quality = 3.16

Bandwidth = 10007.21 

ITheoretical = Vm/sqrt(R^2 +(ωL - 1/ωC)^2) 

              = 3.47/sqrt(100^2+(31622.78*.001-1/(31622.78*100*10^-6))^2 

              =  104.6 mA

IActual = N/A (did not get the image of the current at resonance frequency)

Comparing the two circuits, the angular frequency is smaller in the circuit with the 100Ω resistor and 100µF capacitor than the 10Ω resistor and  1µF capacitor.  This shows that at higher resistance and capacitance, the less frequency is needed to obtain resonance which results in a lower bandwidth.  From the lab, it shows that the lower the resistance and capacitance the higher the bandwidth.

Lab 12 - Low-Pass Filters & High-Pass Filters

Objective:
-Understand the purpose of Low-Pass filters and High-Pass filters in signal processing/modifications.

Lab:
For the lab, the theoretical gain for the low pass was first calculated.

The image above shows the calculations for the theoretical gain and a schematic of the circuit. 

The components that were used for the lab was a function generator, a 1000Ω resistor, and a 1µF capacitor.

The actual values for the 1000Ω resistor = 975Ω and the 1µF capacitor = 1µF.

The input voltage

Low-Pass Filter Results 

The gain is determined by dividing the Output voltage by the Input voltage. 

The results of the Low-Pass filter shows that as frequency increases, the voltage gain within the circuit will eventually reach zero .  

High-Pass Filter Result

The graph for the High-Pass filter shows a slight curve with the top of the curve being the natural response.  From the results, it can be determined that after the high-pass filter passes a certain frequency it begins to decreases.  The graph does not show past 10000 Hz due to the digital multimeter not being able to give good data at higher frequencies.  

Extra Credit: CIE-SoCal Young Engineers and Scientists Professional Forum

Lab 11 - AC Circuit Capacitor

For this lab, Professor Mason hooked up a circuit into a digital oscilloscope to give a visualization of how AC voltage behaves with a capacitor.

Initial sine Wave

Sine wave change as frequency increases

The capacitor that was used in the circuit was about 3.4µF.  The graph shows that as frequency increases, the voltage across the capacitor is decreasing.

(Note: Do not know how to do the calculation to obtain the capacitor, will add later when I figure it out.  The value put is what Professor Mason set the capacitor at for the circuit)

FreeMat Assignment #2

FreeMat screenshots of solving complex numbers.

Lab 10 - Tutorial on Second Order Systems

The lab for this week was a tutorial on Second Order Systems:

The images below are the questions and answers (All in Order)

Total Parts: 18

Lab 9 - Capacitor Charging/Discharging

Objective:
- To test a charge/discharge system that uses a 12 V DC power supply
- Verify if the system charges within 20s with a  resulting stored energy of 2.5 mJ
- Verify if the system will discharge the 2.5 mJ in 2s.

Pre-Circuit Tasks:
The circuit below shows the simple schematic of the charging/discharging system on the capacitor.  To charge/discharge the capacitor, the connected to the positive side of the capacitor is placed in its respective positions.  Meaning the connected cable will be attached to the CHARGE position when the capacitor is to be charged and changed to the DISCHARGE position to discharge.  The rate at the which the energy is transferred is controlled by C, Rcharge, and Rdischarge.

Before determining the values of the components, the expressions for the Thevenin voltage and resistance for the charging and discharging circuits were calculated.

Calculation for Thevenin Expressions

Calculations for Charging/Discharging Circuit Components:

Charging Circuit Component 

Discharging Circuit Component 

The results for the component values:

C = 34.7 µF 

Rcharge = 121212 Ω

Rdischarge = 12121.2 Ω

The Circuit:

Schematic of the Actual Circuit

For each circuit, an oscilloscope was used to show the movement of energy within the circuit.  

Charging Circuit

Charging Circuit

The charging process for the capacitor was about 20 seconds.

The Vfinal obtained after 20secs was about 11.96V.

With the value of Vfinal, RLeak was determined to be 0.145 µΩ.

Discharging Circuit

Discharging Circuit

The discharging circuit did not completely dissipate all its energy within 2 secs. 

Follow up Question

Practical Question: